| |
  
Laboratory of Information Photonics,
Department of Information and Physical Sciences,
Graduate School of Information Science and Technology, Osaka University |
 |
Compressive imaging for multi-dimensional data acquisition
Top (Computational imaging)
Compound-eye camera
Superposition imaging
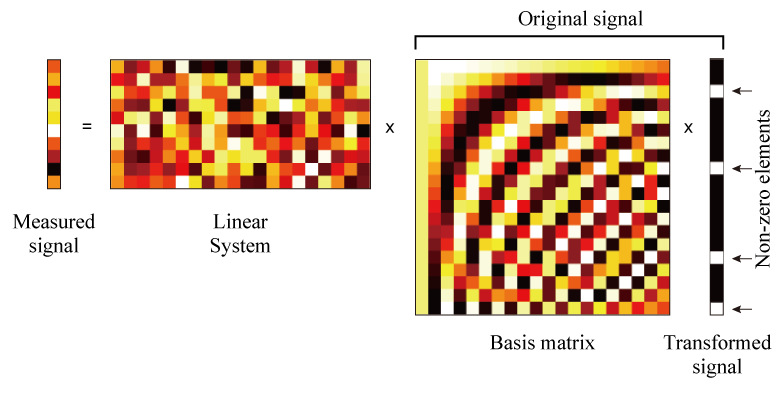
Fig. 1. Compressive sensing |
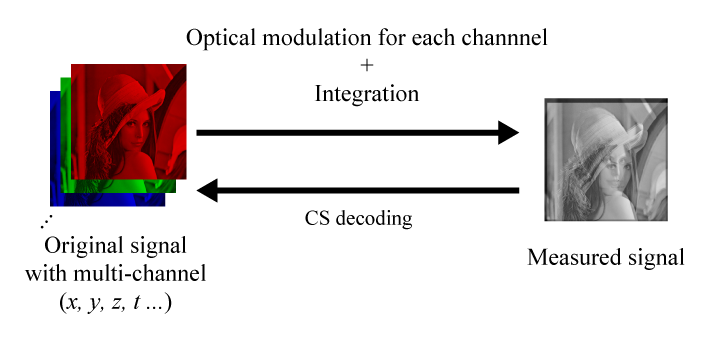
Fig. 2. Multi-dimensional data acquisition based on multiplexing imaging and CS decoding |

Fig. 3. Single-shot wide field-of-view imaging |
|
An image can be expressed as a sparse vector by basis transformation, e.g., the wavelet transform and the DCT.
Based on the compression theory, we can solve inversions of various sensing problems and reconstruct the original signal even if the number of elements of the original signal is larger than that of the measured signal as shown in Fig. 1.
This sensing method is called as compressive sensing (CS) [1] and we have been studying multi-dimensional imaging systems based on CS [2-9].
To acquire a multi-dimensional signal of objects (three-dimensional position, spectrum, polarization, and so on) by single-shot imaging based on CS theory, each channel of the object signal is modulated and multiplexed in the imaging process as described in Fig. 2. The original multi-dimensional signal can be reconstructed by CS decoding. Figure 3 shows an example of compressive imaging, which realizes single-shot wide field-of-view imaging by multiplexing with mirrors and prisms [3].
We have also applied this imaging scheme to active stereo depth sensing [6], holography [7], and reflectance field sensing [8]. These methods have advantages to conventional methods from perspective of high-speed sensing.
|
- D. L. Donoho, “Compressed Sensing,” IEEE Trans. Inform. Theory 25, pp. 1289-1306 (2006).
- R. Horisaki, K. Choi, J. Hahn, J. Tanida, and D. J. Brady, “Generalized sampling using a compound-eye imaging system for multi-dimensional object acquisition,” Opt. Express 18, pp. 19367-19378 (2010).
- R. Horisaki and J. Tanida, “Multi-channel data acquisition using multiplexed imaging with spatial encoding,” Opt. Express 18, pp. 23041-23053 (2010).
- R. Horisaki and J. Tanida, “Preconditioning for multidimensional TOMBO imaging,” Opt. Lett. 36, pp. 2071-2073 (2011).
- R. Horisaki and J. Tanida, “Preconditioning for multiplexed imaging with spatially coded PSFs,” Opt. Express 19, pp. 12540-12550 (2011).
- R. Horisak, N. Fukata, and J. Tanida, “A compressive active stereo imaging system with random pattern projection,” Appl. Phys. Express 5, p. 072501 (2012).
- R. Horisaki, J. Tanida, A. Stern, and B. Javidi, “Multidimensional imaging using compressive Fresnel holography,” Opt. Lett. 37, pp. 2013-2015 (2012).
- R. Horisaki, Y. Tampa, and J. Tanida, “Compressive reflectance field acquisition using confocal imaging with variable coded apertures,” in Proc. of Computational Optical Sensing and Imaging (COSI), CTu3B.4, June 2012 (California).
- R. Horisaki, X. Xiao, J. Tanida, and B. Javidi, “Feasibility study for compressive multi-dimensional integral imaging,” Opt. Express 21, pp. 4263-4279 (2013).
|
|
|
|




